La teoría de sólidos deformables requiere generalmente trabajar con tensiones y deformaciones. Estas magnitudes vienen dadas por campos tensoriales definidos sobre dominios tridimensionales que satisfacen complicadas ecuaciones diferenciales. Sin embargo, para ciertas geometrías aproximadamente unidimensionales (vigas, pilares, celosías, arcos, etc.) o bidimensionales (placas y láminas, membranas, etc.) el estudio puede simplificarse y se pueden analizar mediante el cálculo de esfuerzos internos definidos sobre una línea o una superficie en lugar de tensiones definidas sobre un dominio tridimensional.
La elasticidad es estudiada por la teoría de la elasticidad, que a su vez es parte de la mecánica de sólidos deformables. La teoría de la elasticidad (TE) como la mecánica de sólidos (MS) deformables describe cómo un sólido (o fluido totalmente confinado) se mueve y deforma como respuesta a fuerzas exteriores.
En los materiales elásticos, en particular en muchos metales dúctiles, un esfuerzo uniaxial de tracción pequeño lleva aparejado un comportamiento elástico. Eso significa que pequeños incrementos en la tensión de tracción comporta pequeños incrementos en la deformación, si la carga se vuelve cero de nuevo el cuerpo recupera exactamente su forma original, es decir, se tiene una deformación completamente reversible.
ECUACIÓN CONSTITUTIVA
Las ecuaciones constitutivas de la resistencia de materiales son las que explicitan el comportamiento del material, generalmente se toman como ecuaciones constitutivas las ecuaciones de Lamé-Hooke de la elasticidad lineal. Estas ecuaciones pueden ser especializadas para elementos lineales y superficiales. Para elementos lineales en el cálculo de las secciones, las tensiones sobre cualquier punto (y,z) de la sección puedan escribirse en función de las deformaciones como:
En cambio, para elementos superficiales sometidos predominantemente a flexión como las placas la especialización de las ecuaciones de Hooke es:
Además de ecuaciones constitutivas elásticas, en el cálculo estructural varias normativas recogen métodos de cálculo plástico donde se usan ecuaciones constitutivas de plasticidad.
Esfuerzo normal
El esfuerzo es una medida de la fuerza por unidad de área (en la que se aplica) que
causa la deformación.
Si la fuerza aplicada no es normal ni paralela a la superficie, siempre puede
descomponerse en la suma vectorial de otras dos tal que siempre una sea normal y la
otra paralela a la superficie considerada.
Los esfuerzos con dirección normal a la sección, se denotan normalmente como σ
(sigma) y se denominan como esfuerzo de tracción o tensión cuando apunta hacia
afuera de la sección, tratando de estirar al elemento analizado, y como esfuerzo de
compresión cuando apunta hacia la sección, tratando de aplastar al elemento analizado.
Ley de Hooke.
Cuando estiramos (o comprimimos) un muelle, la fuerza recuperadora es directamente
proporcional a la deformación x (al cambio de longitud x respecto de la posición de
equilibrio) y de signo contraria a ésta. F = - k x, Siendo k una constante de
proporcionalidad, denominada constante elástica del muelle. El signo menos en la
ecuación anterior se debe a que la fuerza recuperadora es opuesta a la deformación
La ley de Hooke es solo aplicable a deformaciones unitarias pequeñas, hasta que se
alcanza el límite de proporcionalidad (ver figura).
En las curvas esfuerzo - deformación de un material hay un tramo de comportamiento
perfectamente elástico en el que la relación esfuerzo – deformación es lineal (punto
A). De ahí hasta otro punto B (de límite elástico) el material sigue un comportamiento
elástico (sigue habiendo una relación entre esfuerzo y deformación, aunque no es lineal,
y si se retira el esfuerzo se recupera la longitud inicial). Si se sigue aumentando la
carga (por encima del punto b hasta el punto B’ ), el material se deforma rápidamente y
si se retira el esfuerzo no se recupera la longitud inicial, quedando una deformación
permanente y el cuerpo tiene un comportamiento plástico.
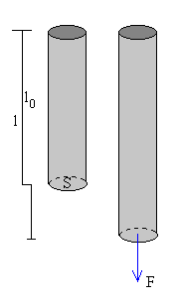
Deformación por tracción o compresión. Módulo de
Young.
Si aplicamos una fuerza F a una barra de longitud l0 el
material se deforma longitudinalmente y se alarga l - l0. La razón de proporcionalidad entre el esfuerzo (fuerza por
unidad de área) y deformación unitaria (deformación por
unidad de longitud) está dada por la constante E, denominada
módulo de Young , que es característico de cada material.
Cizalladura. Módulo de rigidez
Hasta hora solo hemos tenido en cuenta fuerzas normales a las superficies que dan
lugar a esfuerzos normales y a deformaciones de volumen. Supongamos ahora que las
fuerzas F que se aplican son tangenciales a una superficie A, el cambio que se produce
en el cuerpo es solo un cambio de forma ya que el volumen permanece constante.
El esfuerzo cortante o tangencial τ, es la fuerza de corte o tangencial por unidad de
área:
Cuando actúan esfuerzos cortantes el material se deforma como si el material (p.e. un
cubo) estuviera formado por láminas paralelas y se deformaran como lo haría el libro de
la figura; a esta deformación que supone un deslizamiento según el esfuerzo cortante o
de cizalladura se denomina deformación cortante, angular o de cizalladura y vale:
donde G se denomina módulo de elasticidad tangencial o más habitualmente módulo de
rigidez (o también módulo de cortante o de cizalladura ).
La deformación por cizalladura se produce sólo en los sólidos, por eso se dice que
estos presentan rigidez. Los sólidos pueden tener deformaciones volumétricas y de
forma, mientras que los fluidos solo tienen deformación volumétrica.
La relación esfuerzo cortante –deformación de cizalladura, en un estado bidimensional
de cizalladura pura, cumple, dentro de los límites elásticos de la ley de Hooke, una
relación del tipo: